6 Numerisches Rechnen mit Python und Numpy

Dieses Tutorial ist das fünfte in einer Reihe zur Einführung in die Programmierung und Datenanalyse mithilfe der Python-Programmiersprache. Diese Tutorials basieren auf einem praktischen, programmbasierten Ansatz. Der beste Weg, das Material zu erlernen, besteht darin, den Code auszuführen und mit den Beispielen zu experimentieren.

Die folgenden Themen werden in diesem Tutorial behandelt:

Arbeiten mit numerischen Daten
Von Python-Listen zu Numpy-Arrays wechseln
Umgang mit Numpy-Arrays
Vorteile der Verwendung von Numpy-Arrays
Mehrdimensionale Numpy-Arrays
Arbeiten mit CSV-Dateien
Arithmetische Operationen und Broadcasting
Array-Indizierung und Slicing
Andere Möglichkeiten zum Erstellen von Numpy-Arrays

6.1 Arbeiten mit numerischen Daten

Die “Daten” in der Datenanalyse beziehen sich in der Regel auf numerische Daten, wie z. B. Aktienkurse, Verkaufszahlen, Sensormessungen, Sportergebnisse, Datenbanktabellen usw. Die Numpy-Bibliothek bietet spezialisierte Datenstrukturen, Funktionen und andere Tools für numerische Berechnungen in Python. Lassen Sie uns ein Beispiel durchgehen, um zu sehen, warum und wie Numpy für die Arbeit mit numerischen Daten verwendet wird.

Nehmen wir an, wir möchten Klimadaten wie die Temperatur, den Niederschlag und die Luftfeuchtigkeit in einer Region nutzen, um festzustellen, ob die Region gut geeignet ist, um Äpfel anzubauen. Ein wirklich einfacher Ansatz dafür wäre, die Beziehung zwischen dem jährlichen Apfelertrag (Tonnen pro Hektar) und den klimatischen Bedingungen wie der Durchschnittstemperatur (in Grad Fahrenheit), dem Niederschlag (in Millimetern) und der durchschnittlichen relativen Luftfeuchtigkeit (in Prozent) als lineare Gleichung zu formulieren.

apfelertrag = w1 * temperatur + w2 * niederschlag + w3 * luftfeuchtigkeit

Wir drücken den Ertrag an Äpfeln als gewichtete Summe der Temperatur, des Niederschlags und der Luftfeuchtigkeit aus. Offensichtlich ist dies eine Annäherung, da die tatsächliche Beziehung nicht unbedingt linear sein muss. Aber ein einfaches lineares Modell wie dieses funktioniert oft gut in der Praxis.

Auf der Grundlage einiger statistischer Analysen historischer Daten könnten wir in der Lage sein, vernünftige Werte für die Gewichte w1, w2 und w3 zu ermitteln. Hier ist ein Beispiel für einen Satz von Werten:

Code

w1, w2, w3 = 0.3, 0.2, 0.5

Anhand einiger Klimadaten für eine Region können wir nun vorhersagen, wie der Apfelertrag in der Region aussehen könnte. Hier sind einige Beispieldaten:

Zunächst können wir einige Variablen definieren, um die Klimadaten für eine Region aufzuzeichnen.

Code

kanto_temp = 73
kanto_rainfall = 67
kanto_humidity = 43

Diese Variablen können wir nun in die lineare Gleichung einsetzen, um den Apfelertrag in dieser Region vorherzusagen.

Code

kanto_yield_apples = kanto_temp * w1 + kanto_rainfall * w2 + kanto_humidity * w3
kanto_yield_apples

56.8

Code

print("The expected yield of apples in Kanto region is {} tons per hectare.".format(kanto_yield_apples))

The expected yield of apples in Kanto region is 56.8 tons per hectare.

Um die Durchführung der obigen Berechnung für mehrere Regionen etwas zu vereinfachen, können wir die Klimadaten für jede Region als Vektor, also als Zahlenliste, darstellen.

Code

kanto = [73, 67, 43]
johto = [91, 88, 64]
hoenn = [87, 134, 58]
sinnoh = [102, 43, 37]
unova = [69, 96, 70]

Die drei Zahlen in jedem Vektor repräsentieren jeweils die Temperatur-, Niederschlags- und Luftfeuchtigkeitsdaten. Der im Forum zu verwendende Gewichtungssatz kann auch als Vektor dargestellt werden.

Code

weights = [w1, w2, w3]

Wir können jetzt eine Funktion crop_yield schreiben, um den Ertrag von Äpfeln (oder einer anderen Ernte) unter Berücksichtigung der Klimadaten und der jeweiligen Gewichte zu berechnen.

Code

kanto

[73, 67, 43]

Code

weights

[0.3, 0.2, 0.5]

Code

for item in zip(kanto, weights):
  print(item)

(73, 0.3)
(67, 0.2)
(43, 0.5)

Code

result = 0
for x, w in zip(kanto, weights):
  print(x * w)
  result += x * w
print(result)

21.9
13.4
21.5
56.8

Code

def crop_yield(region, weights):
    result = 0
    for x, w in zip(region, weights):
        result += x * w
    return result

Code

crop_yield(kanto, weights)

56.8

Code

crop_yield(johto, weights)

76.9

Code

crop_yield(unova, weights)

74.9

6.2 Von Python-Listen zu Numpy-Arrays wechseln

Die durch crop_yield (elementweise Multiplikation zweier Vektoren und Bildung einer Summe der Ergebnisse) durchgeführte Berechnung wird auch als Skalarprodukt der beiden Vektoren bezeichnet.

Die Numpy-Bibliothek bietet eine integrierte Funktion zum Berechnen des Skalarprodukts zweier Vektoren. Allerdings müssen die Listen zunächst in Numpy-Arrays konvertiert werden, bevor wir die Operation ausführen können. Zunächst importieren wir das Modul numpy. Es ist üblich, Numpy mit dem Alias np zu importieren.

Bevor die Numpy-Bibliothek nutzen können, müssen wir sie mit Hilfe des Python Paketverwaltungsprogramm pip installieren, da es ich beim Numpy um keine built-in Standardbibliothek handelt.

Code

!pip install numpy

Requirement already satisfied: numpy in /Users/christianjulianebert/anaconda3/lib/python3.10/site-packages (1.23.5)

Code

import numpy as np

Numpy-Arrays können mit der Funktion np.array erstellt werden.

Code

kanto = np.array([73, 67, 43])

Code

kanto

array([73, 67, 43])

Code

weights = np.array([w1, w2, w3])

Code

weights

array([0.3, 0.2, 0.5])

Code

type(kanto)

numpy.ndarray

Code

type(weights)

numpy.ndarray

Genau wie Listen unterstützen Numpy-Arrays die Indexierungsnotation [].

Code

weights[0]

0.3

Code

kanto[2]

6.3 Umgang mit Numpy-Arrays

Wir können nun das Skalarprodukt der beiden Vektoren mit der Funktion np.dot berechnen

Code

np.dot(kanto, weights)

56.8

Das gleiche Ergebnis können wir mit Operationen auf niedrigerer Ebene erzielen, die von Numpy-Arrays unterstützt werden: Durchführen einer elementweisen Multiplikation und Berechnen der Summe der resultierenden Zahlen.

Code

(kanto * weights).sum()

56.8

Der *-Operator führt eine elementweise Multiplikation zweier Arrays durch (vorausgesetzt, sie haben die gleiche Größe), und die sum Methode berechnet die Summe der Zahlen in einem Array.

Code

arr1 = np.array([1, 2, 3])
arr2 = np.array([4, 5, 6])

Code

arr1 * arr2

array([ 4, 10, 18])

Code

arr2.sum()

6.4 Vorteile der Verwendung von Numpy-Arrays

Es gibt ein paar wichtige Vorteile bei der Verwendung von Numpy-Arrays anstelle von Python-Listen zur Bearbeitung von numerischen Daten:

Benutzerfreundlichkeit: Sie können kleine, prägnante und intuitive mathematische Ausdrücke wie (kanto * weights).sum() schreiben, anstatt Schleifen und benutzerdefinierte Funktionen wie crop_yield zu verwenden.
Leistung: Numpy-Operationen und -Funktionen sind intern in C++ implementiert, was sie viel schneller macht als Python-Anweisungen und -Schleifen, die zur Laufzeit interpretiert werden

Hier ist ein schneller Vergleich von Skalarprodukten, die mit Vektoren mit jeweils einer Million Elementen durchgeführt werden, und zwar mit Python-Schleifen im Vergleich zu Numpy-Arrays.

Code

# Python lists
arr1 = list(range(1000000))
arr2 = list(range(1000000, 2000000))

# Numpy arrays
arr1_np = np.array(arr1)
arr2_np = np.array(arr2)

Code

%%time
result = 0
for x1, x2 in zip(arr1, arr2):
    result += x1*x2
print(result)

833332333333500000
CPU times: user 94.6 ms, sys: 1.57 ms, total: 96.2 ms
Wall time: 95 ms

Code

%%time
np.dot(arr1_np, arr2_np)

CPU times: user 1.29 ms, sys: 1.09 ms, total: 2.38 ms
Wall time: 1.08 ms

833332333333500000

Wie Sie sehen, ist die Verwendung von np.dot 100-mal schneller als die Verwendung einer for-Schleife. Dies macht Numpy besonders nützlich, wenn mit wirklich großen Datensätzen mit Zehntausenden oder Millionen Datenpunkten gearbeitet wird.

6.5 Mehrdimensionale Numpy-Arrays

Wir können nun noch einen Schritt weiter gehen und die Klimadaten für alle Regionen gemeinsam in einem einzigen zweidimensionalen Numpy-Array darstellen.

Code

climate_data = np.array([[73, 67, 43],
                         [91, 88, 64],
                         [87, 134, 58],
                         [102, 43, 37],
                         [69, 96, 70]])

Code

climate_data

array([[ 73,  67,  43],
       [ 91,  88,  64],
       [ 87, 134,  58],
       [102,  43,  37],
       [ 69,  96,  70]])

Wenn Sie in der High School einen Kurs über lineare Algebra besucht haben, erkennen Sie das obige zweidimensionale Array vielleicht als eine Matrix mit 5 Zeilen (eine für jede Region) und 3 Spalten (die Werte für Temperatur und Niederschlag enthalten). und Luftfeuchtigkeit).

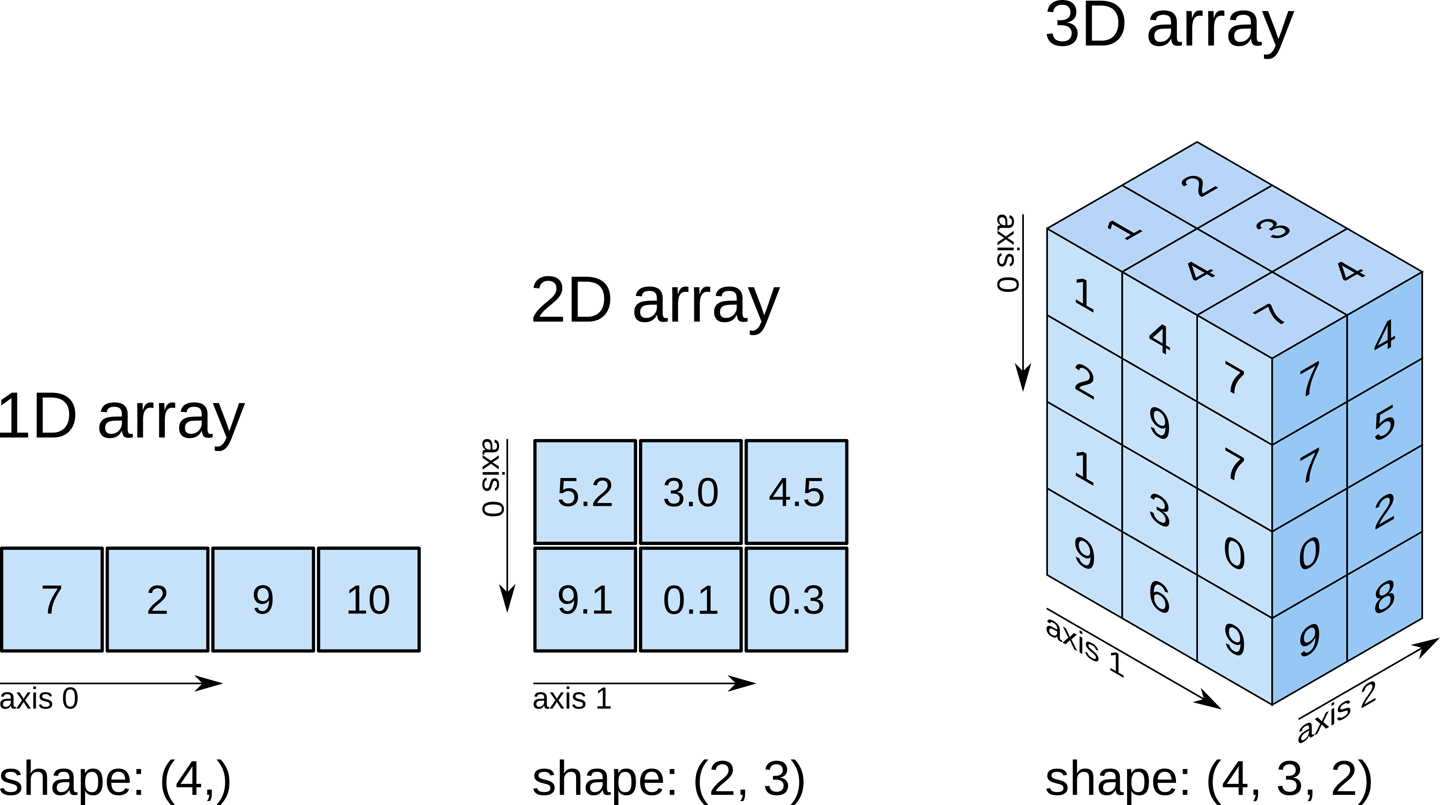
Numpy-Arrays können beliebig viele Dimensionen und unterschiedliche Längen entlang jeder Dimension haben. Mit der Eigenschaft .shape eines Arrays können wir die Länge entlang jeder Dimension überprüfen.

Code

climate_data

array([[ 73,  67,  43],
       [ 91,  88,  64],
       [ 87, 134,  58],
       [102,  43,  37],
       [ 69,  96,  70]])

Code

# 2D array (matrix)
climate_data.shape

(5, 3)

Code

weights

array([0.3, 0.2, 0.5])

Code

# 1D array (vector)
weights.shape

(3,)

Code

# 3D array 
arr3 = np.array([
                 [[11, 12, 13], 
                  [13, 14, 15]], 

                 [[15, 16, 17], 
                  [17, 18, 19.5]]
                                 ])

Code

arr3.shape

(2, 2, 3)

Alle Elemente in einem Numpy-Array haben denselben Datentyp. Sie können den Datentyp eines Arrays mithilfe der Eigenschaft .dtype überprüfen

Code

weights.dtype

dtype('float64')

Code

climate_data.dtype

dtype('int64')

Wenn ein Array auch nur eine einzelne Gleitkommazahl enthält, werden alle anderen Elemente ebenfalls in Gleitkommazahlen umgewandelt.

Code

arr3.dtype

dtype('float64')

Code

climate_data

array([[ 73,  67,  43],
       [ 91,  88,  64],
       [ 87, 134,  58],
       [102,  43,  37],
       [ 69,  96,  70]])

Wir können nun die vorhergesagten Apfelerträge in allen Regionen berechnen, indem wir eine einzelne Matrixmultiplikation zwischen climate_data (einer 5x3-Matrix) und weights (einem Vektor der Länge 3) verwenden. So sieht es optisch aus:

Wir können die Funktion np.matmul von Numpy verwenden oder einfach den Operator @ verwenden, um eine Matrixmultiplikation durchzuführen.

Code

climate_data

array([[ 73,  67,  43],
       [ 91,  88,  64],
       [ 87, 134,  58],
       [102,  43,  37],
       [ 69,  96,  70]])

Code

weights

array([0.3, 0.2, 0.5])

Code

np.matmul(climate_data, weights)

array([56.8, 76.9, 81.9, 57.7, 74.9])

Code

climate_data @ weights

array([56.8, 76.9, 81.9, 57.7, 74.9])

6.6 Arbeiten mit CSV-Dateien

Numpy bietet auch Hilfsfunktionen zum Lesen von und Schreiben in Dateien an. Lassen Sie uns eine Datei climate.txt herunterladen, die 10.000 Klimadaten (Temperatur, Niederschlag & Luftfeuchtigkeit) im folgenden Format enthält:

Temperatur,Niederschlag,Luftfeuchtigkeit
25,00,76,00,99,00
39,00,65,00,70,00
59,00,45,00,77,00
84,00,63,00,38,00
66,00,50,00,52,00
41,00,94,00,77,00
91,00,57,00,96,00
49,00,96,00,99,00
67,00,20,00,28,00
...

Diese Art der Datenspeicherung ist bekannt als Comma Separated Values oder CSV.

CSVs: Eine Datei mit durch Kommas getrennten Werten (CSV) ist eine Textdatei, die ein Komma zur Trennung von Werten verwendet. Jede Zeile der Datei ist ein Datensatz. Jeder Datensatz besteht aus einem oder mehreren Feldern, die durch Kommas getrennt sind. Eine CSV-Datei speichert typischerweise tabellarische Daten (Zahlen und Text) im Klartext, in diesem Fall hat jede Zeile die gleiche Anzahl von Feldern. (Wikipedia)

Um diese Datei in ein Numpy-Array zu lesen, können wir die Funktion genfromtxt verwenden.

Code

climate_data = np.genfromtxt('data/climate.txt', delimiter=',', skip_header=1)

Code

climate_data

array([[25., 76., 99.],
       [39., 65., 70.],
       [59., 45., 77.],
       ...,
       [99., 62., 58.],
       [70., 71., 91.],
       [92., 39., 76.]])

Code

climate_data.shape

(10000, 3)

Wir können jetzt einen Matrix-Mulplikationsoperator @ verwenden, um den Apfelertrag für den gesamten Datensatz unter Verwendung eines gegebenen Satzes von Gewichten vorherzusagen.

Code

weights = np.array([0.3, 0.2, 0.5])

Code

yields = climate_data @ weights

Code

yields

array([72.2, 59.7, 65.2, ..., 71.1, 80.7, 73.4])

Code

yields.shape

(10000,)

Mit der Funktion np.concatenate können wir nun die yields als vierte Spalte wieder zu climate_data hinzufügen .

Code

climate_results = np.concatenate((climate_data, yields.reshape(10000, 1)), axis=1)

Code

climate_results

array([[25. , 76. , 99. , 72.2],
       [39. , 65. , 70. , 59.7],
       [59. , 45. , 77. , 65.2],
       ...,
       [99. , 62. , 58. , 71.1],
       [70. , 71. , 91. , 80.7],
       [92. , 39. , 76. , 73.4]])

Es gibt hier ein paar Feinheiten:

Wir müssen das Argument axis für np.concatenate bereitstellen, um die Dimension zu spezifizieren, entlang der die Konkatenation ausgeführt werden soll.
Die zu konkatenierenden Arrays sollten die gleiche Anzahl von Dimensionen und die gleiche Länge entlang jeder Dimension haben, außer derjenigen, entlang der die Konkatenation durchgeführt wird. Wir verwenden hier die Funktion np.reshape, um die Form von yields von (10000,) auf (10000,1) zu ändern.

Hier ist eine visuelle Erklärung von np.concatenate entlang axis=1 (können Sie erraten, was axis=0 ergibt?):

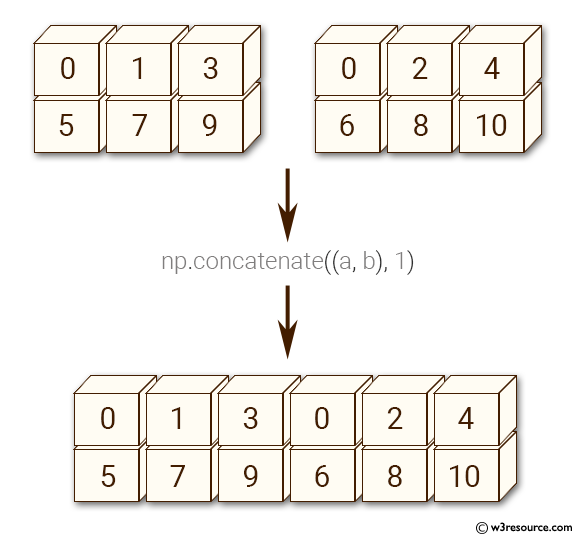
Der beste Weg, um zu verstehen, was eine Numpy-Funktion tut, besteht darin, mit ihr zu experimentieren und die Dokumentation mit der Funktion help zu lesen, um mehr über ihre Argumente und Rückgabewerte zu erfahren. Nutzen Sie die folgenden Zellen, um mit np.concatenate und np.reshape zu experimentieren.

Code

# Tragen Sie hier Ihren Code ein!

Schreiben wir die Endergebnisse unserer obigen Berechnung mit der Funktion np.savetxt zurück in eine Datei, die sich im data Ordner befinden soll.

Code

climate_results

array([[25. , 76. , 99. , 72.2],
       [39. , 65. , 70. , 59.7],
       [59. , 45. , 77. , 65.2],
       ...,
       [99. , 62. , 58. , 71.1],
       [70. , 71. , 91. , 80.7],
       [92. , 39. , 76. , 73.4]])

Code

np.savetxt('data/climate_results.txt', 
           climate_results, 
           fmt='%.2f', 
           header='temperature,rainfall,humidity,yeild_apples', 
           comments='')

Code

np.savetxt('data/climate_results_nocomments.txt', 
           climate_results, 
           fmt='%.2f', 
           header='temperature,rainfall,humidity,yeild_apples')

Die Ergebnisse werden im CSV-Format in die Datei climate_results.txt zurückgeschrieben.

Temperatur,Niederschlag,Luftfeuchtigkeit
25.00 76.00 99.00 72.20
39.00 65.00 70.00 59.70
59.00 45.00 77.00 65.20
84.00 63.00 38.00 56.80
66.00 50.00 52.00 55.80
41.00 94.00 77.00 69.60
91.00 57.00 96.00 86.70
49.00 96.00 99.00 83.40
67.00 20.00 28.00 38.10
...

Numpy bietet Hunderte von Funktionen zum Ausführen von Operationen an Arrays. Hier sind einige allgemeine Funktionen:

Mathematik: np.sum, np.exp, np.round, arithemtische Operatoren Array-Manipulation: np.reshape, np.stack, np.concatenate, np.split Lineare Algebra: np.matmul, np.dot, np.transpose, np.eigvals Statistiken: np.mean, np.median, np.std, np.max

Wie finden Sie die Funktion, die Sie benötigen? Da Numpy Hunderte von Funktionen zum Bearbeiten von Arrays bietet, kann es manchmal schwierig sein, genau das zu finden, was Sie benötigen. Der einfachste Weg, die richtige Funktion zu finden, ist eine Websuche, z. B. Die Suche nach „So verknüpfen Sie Numpy-Arrays“ führt zu diesem Tutorial zur Array-Verkettung.

Eine vollständige Liste der Array-Funktionen finden Sie hier.

6.7 Arithmetische Operationen und Broadcasting

Numpy-Arrays unterstützen arithmetische Operatoren wie +, -, * usw. Sie können eine arithmetische Operation mit einer einzelnen Zahl (auch Skalar genannt) oder mit einem anderen Array derselben Form ausführen. Dadurch ist es wirklich einfach, mathematische Ausdrücke mit mehrdimensionalen Arrays zu schreiben.

Code

arr2 = np.array([[1, 2, 3, 4], 
                 [5, 6, 7, 8], 
                 [9, 1, 2, 3]])

Code

arr3 = np.array([[11, 12, 13, 14], 
                 [15, 16, 17, 18], 
                 [19, 11, 12, 13]])

Code

arr2 + arr3

array([[12, 14, 16, 18],
       [20, 22, 24, 26],
       [28, 12, 14, 16]])

Code

# Adding a scalar
arr2 + 3

array([[ 4,  5,  6,  7],
       [ 8,  9, 10, 11],
       [12,  4,  5,  6]])

Code

# Element-wise subtraction
arr3 - arr2

array([[10, 10, 10, 10],
       [10, 10, 10, 10],
       [10, 10, 10, 10]])

Code

# Division by scalar
arr2 / 2

array([[0.5, 1. , 1.5, 2. ],
       [2.5, 3. , 3.5, 4. ],
       [4.5, 0.5, 1. , 1.5]])

Code

# Element-wise multiplication
arr2 * arr3

array([[ 11,  24,  39,  56],
       [ 75,  96, 119, 144],
       [171,  11,  24,  39]])

Code

# Modulus with scalar or find the reminder
arr2 % 4

array([[1, 2, 3, 0],
       [1, 2, 3, 0],
       [1, 1, 2, 3]])

Numpy-Arrays unterstützen auch Broadcasting, was arithmetische Operationen zwischen zwei Arrays mit unterschiedlicher Anzahl an Dimensionen, aber kompatiblen Formen ermöglicht. Schauen wir uns ein Beispiel an, um zu sehen, wie es funktioniert.

Code

arr2 = np.array([[1, 2, 3, 4], 
                 [5, 6, 7, 8], 
                 [9, 1, 2, 3]])

Code

arr2.shape

(3, 4)

Code

arr4 = np.array([4, 5, 6, 7])

Code

arr4_replicate = np.array([[4, 5, 6, 7],
                           [4, 5, 6, 7],
                           [4, 5, 6, 7]])

Code

arr4_replicate.shape

(3, 4)

Code

arr4.shape

(4,)

Code

arr2 + arr4

array([[ 5,  7,  9, 11],
       [ 9, 11, 13, 15],
       [13,  6,  8, 10]])

Code

arr2 + arr4_replicate

array([[ 5,  7,  9, 11],
       [ 9, 11, 13, 15],
       [13,  6,  8, 10]])

Wenn der Ausdruck arr2 + arr4 ausgewertet wird, wird arr4 (das die Form (4,) hat) dreimal repliziert, um der Form (3, 4) von arr2 zu entsprechen. Dies ist sehr nützlich, da Numpy die Replikation durchführt, ohne tatsächlich drei Kopien des Arrays mit der kleineren Dimension zu erstellen.

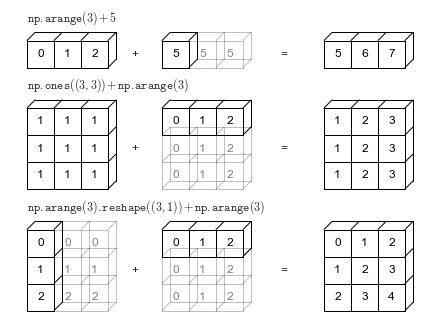
Broadcasting funktioniert nur, wenn eines der Arrays so repliziert werden kann, dass es genau der Form des anderen Arrays entspricht.

Code

arr5 = np.array([7, 8])

Code

arr5.shape

(2,)

Code

arr5_replicated = np.array([[7, 8],
                            [7, 8],
                            [7, 8]])

Code

arr2 + arr5

---------------------------------------------------------------------------
ValueError                                Traceback (most recent call last)
Cell In[80], line 1
----> 1 arr2 + arr5

ValueError: operands could not be broadcast together with shapes (3,4) (2,)

Selbst wenn arr5 im obigen Beispiel dreimal repliziert wird, stimmt es nicht mit der Form von arr2 überein, daher kann arr2 + arr5 nicht erfolgreich ausgewertet werden. Erfahren Sie hier mehr über Broadcasting.

Numpy-Arrays unterstützen auch Vergleichsoperationen wie ==, !=, > usw. Das Ergebnis ist ein Array von booleschen Werten.

Code

arr1 = np.array([[1, 2, 3], [3, 4, 5]])
arr2 = np.array([[2, 2, 3], [1, 2, 5]])

Code

arr1 == arr2

array([[False,  True,  True],
       [False, False,  True]])

Code

(arr1 == arr2).dtype

dtype('bool')

Code

arr1 != arr2

array([[ True, False, False],
       [ True,  True, False]])

Code

arr1 >= arr2

array([[False,  True,  True],
       [ True,  True,  True]])

Code

arr1 < arr2

array([[ True, False, False],
       [False, False, False]])

Ein häufiger Anwendungsfall hierfür ist das Zählen der Anzahl gleicher Elemente in zwei Arrays mithilfe der sum-Methode. Denken Sie daran, dass True den Wert 1 und False den Wert 0 ergibt, wenn boolesche Werte in arithmetischen Operationen verwendet werden.

Code

(arr1 == arr2).sum()

6.8 Array-Indizierung und Slicing

Numpy erweitert die Listenindizierungsnotation von Python mithilfe von [] auf ziemlich intuitive Weise auf mehrere Dimensionen. Sie können eine durch Kommas getrennte Liste von Indizes oder Bereichen bereitstellen, um ein bestimmtes Element oder ein Subarray (auch Slice genannt) aus einem Numpy-Array auszuwählen.

Code

arr3 = np.array([
    [[11, 12, 13, 14], 
     [13, 14, 15, 19]], 
    
    [[15, 16, 17, 21], 
     [63, 92, 36, 18]], 
    
    [[98, 32, 81, 23],      
     [17, 18, 19.5, 43]]])

Code

arr3.shape

(3, 2, 4)

Code

# Single element
arr3[1, 1, 2]

36.0

Code

arr3[1, 1, 2]

36.0

Code

arr3

array([[[11. , 12. , 13. , 14. ],
        [13. , 14. , 15. , 19. ]],

       [[15. , 16. , 17. , 21. ],
        [63. , 92. , 36. , 18. ]],

       [[98. , 32. , 81. , 23. ],
        [17. , 18. , 19.5, 43. ]]])

Code

arr3[1:]

array([[[15. , 16. , 17. , 21. ],
        [63. , 92. , 36. , 18. ]],

       [[98. , 32. , 81. , 23. ],
        [17. , 18. , 19.5, 43. ]]])

Code

arr3[1:, 0:1]

array([[[15., 16., 17., 21.]],

       [[98., 32., 81., 23.]]])

Code

# Subarray using ranges
arr3[1:, 0:1, :2]

array([[[15., 16.]],

       [[98., 32.]]])

Code

arr3

array([[[11. , 12. , 13. , 14. ],
        [13. , 14. , 15. , 19. ]],

       [[15. , 16. , 17. , 21. ],
        [63. , 92. , 36. , 18. ]],

       [[98. , 32. , 81. , 23. ],
        [17. , 18. , 19.5, 43. ]]])

Code

arr3[1:]

array([[[15. , 16. , 17. , 21. ],
        [63. , 92. , 36. , 18. ]],

       [[98. , 32. , 81. , 23. ],
        [17. , 18. , 19.5, 43. ]]])

Code

arr3[1:, 1]

array([[63. , 92. , 36. , 18. ],
       [17. , 18. , 19.5, 43. ]])

Code

# Mixing indices and ranges
arr3[1:, 1, 3]

array([18., 43.])

Code

# Mixing indices and ranges
arr3[1:, 1, :3]

array([[63. , 92. , 36. ],
       [17. , 18. , 19.5]])

Code

# Using fewer indices
arr3[1]

array([[15., 16., 17., 21.],
       [63., 92., 36., 18.]])

Code

# Using fewer indices
arr3[:2, 1]

array([[13., 14., 15., 19.],
       [63., 92., 36., 18.]])

Code

# Using too many indices
arr3[1,3,2,1]

---------------------------------------------------------------------------
IndexError                                Traceback (most recent call last)
Cell In[103], line 2
      1 # Using too many indices
----> 2 arr3[1,3,2,1]

IndexError: too many indices for array: array is 3-dimensional, but 4 were indexed

Die Notation und die Ergebnisse können zunächst verwirrend sein. Nehmen Sie sich also Zeit zum Experimentieren und machen Sie sich damit vertraut. Verwenden Sie die folgenden Zellen, um einige Beispiele für die Indexierung und Aufteilung von Arrays mit verschiedenen Kombinationen von Indizes und Bereichen auszuprobieren. Hier sind einige weitere Beispiele, die visuell veranschaulicht werden:

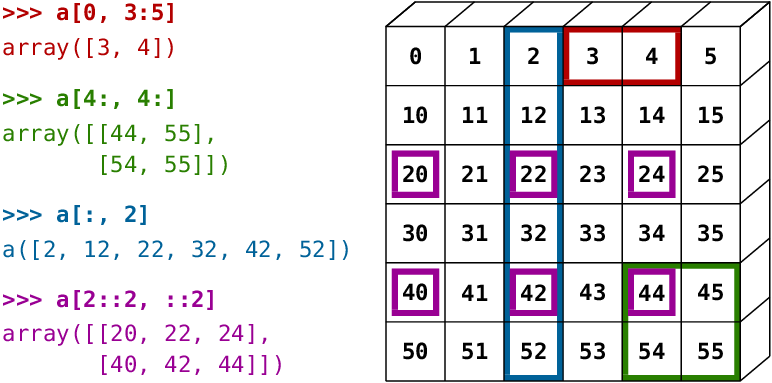
6.9 Andere Möglichkeiten zum Erstellen von Numpy-Arrays

Numpy bietet außerdem einige praktische Funktionen zum Erstellen von Arrays einer gewünschten Form mit festen oder zufälligen Werten. Schauen Sie sich die offizielle Dokumentation an oder nutzen Sie die help-Funktion, um mehr über die folgenden Funktionen zu erfahren.

Code

# All zeros
np.zeros((3, 2))

array([[0., 0.],
       [0., 0.],
       [0., 0.]])

Code

# All ones
np.ones([2, 2, 3])

array([[[1., 1., 1.],
        [1., 1., 1.]],

       [[1., 1., 1.],
        [1., 1., 1.]]])

Code

# Identity matrix
np.eye(3)

array([[1., 0., 0.],
       [0., 1., 0.],
       [0., 0., 1.]])

Code

# Random vector
np.random.rand(5)

array([0.57946642, 0.1520226 , 0.26882721, 0.59721361, 0.77004381])

Code

# Random matrix
np.random.randn(2, 3) # rand vs. randn - what's the difference?

array([[ 0.22724674, -0.15781586,  0.22040568],
       [-0.69069408, -0.89697522, -0.86484168]])

Code

# Fixed value
np.full([2, 3], 42)

array([[42, 42, 42],
       [42, 42, 42]])

Code

# Range with start, end and step
np.arange(10, 90, 3)

array([10, 13, 16, 19, 22, 25, 28, 31, 34, 37, 40, 43, 46, 49, 52, 55, 58,
       61, 64, 67, 70, 73, 76, 79, 82, 85, 88])

Code

np.arange(10, 90, 3).shape

(27,)

Code

np.arange(10, 90, 3).reshape(3,3,-1)

array([[[10, 13, 16],
        [19, 22, 25],
        [28, 31, 34]],

       [[37, 40, 43],
        [46, 49, 52],
        [55, 58, 61]],

       [[64, 67, 70],
        [73, 76, 79],
        [82, 85, 88]]])

Code

# Equally spaced numbers in a range
np.linspace(3, 27, 9)

array([ 3.,  6.,  9., 12., 15., 18., 21., 24., 27.])

6.1 Arbeiten mit numerischen Daten

6.2 Von Python-Listen zu Numpy-Arrays wechseln

6.3 Umgang mit Numpy-Arrays

6.4 Vorteile der Verwendung von Numpy-Arrays

6.5 Mehrdimensionale Numpy-Arrays

6.6 Arbeiten mit CSV-Dateien

6.7 Arithmetische Operationen und Broadcasting

6.8 Array-Indizierung und Slicing

6.9 Andere Möglichkeiten zum Erstellen von Numpy-Arrays

6.10 Weiterführende Literatur